In sommige bronnen is er iets aan de hand als het belang van de volgorde van de toepassing van rollen, stampen en gieren. Maar ik kan niet begrijpen waarom dit verband houdt.

Neem uw rechterhand: wijs uw duim naar boven, uw wijsvinger van u af en uw middelvinger naar links. Je hebt nu een rechtshandig coördinatensysteem: je duim is de x-as, je wijsvinger de y-as en je middelvinger de z-as.

Draai eerst + 90 ° rond de x-as (duim). Uw wijsvinger wijst nu naar links en uw middelvinger naar u toe. Draai vervolgens + 90 ° rond de y-as (wijsvinger). Je duim wijst nu van je af, je wijsvinger naar links en je middelvinger naar boven.

Ga nu terug naar de beginpositie en pas dezelfde twee rotaties in een andere volgorde toe, eerst rond de y-as en vervolgens de x-as: + 90 ° roteren rond de y-as (wijsvinger). Je duim wijst nu naar rechts, je wijsvinger van je af en je middelvinger naar boven. Draai vervolgens + 90 ° rond de x-as (duim). Je duim wijst nu naar rechts, je wijsvinger naar boven en je middelvinger naar je toe.

Dit is anders dan het laatste resultaat: volgorde van rotatie is belangrijk.

Ik heb accelerometerwaarden gebruikt door ze in een aantal formules op internet in te voeren (die arctangens-formules, die iedereen gebruikt, maar niemand legt het goed uit)

Wanneer het vliegtuig met een constante snelheid beweegt, wordt de accelerometer meet alleen de versnelling als gevolg van de zwaartekracht, een vector die precies naar beneden wijst, (0, 0, -g) in het globale coördinatensysteem. Dit is altijd waar, ongeacht de oriëntatie van de sensor.
Als de sensor perfect waterpas staat, is het lokale coördinatensysteem van de sensor uitgelijnd met het globale coördinatensysteem, zodat de sensor ook meet (0, 0, -g).

Wanneer de sensor gekanteld is, heeft de gemeten vector ook een x- en y-component.
Om het simpel te houden, stel je het geval voor waarin de sensor rond de positieve y-as is gekanteld.
De sensor meet nu zowel een x-component als een az-component: (x, 0, -z).

Zoals je kunt zien in de volgende afbeelding, is de rotatiehoek θ = atan2 (x, z) .

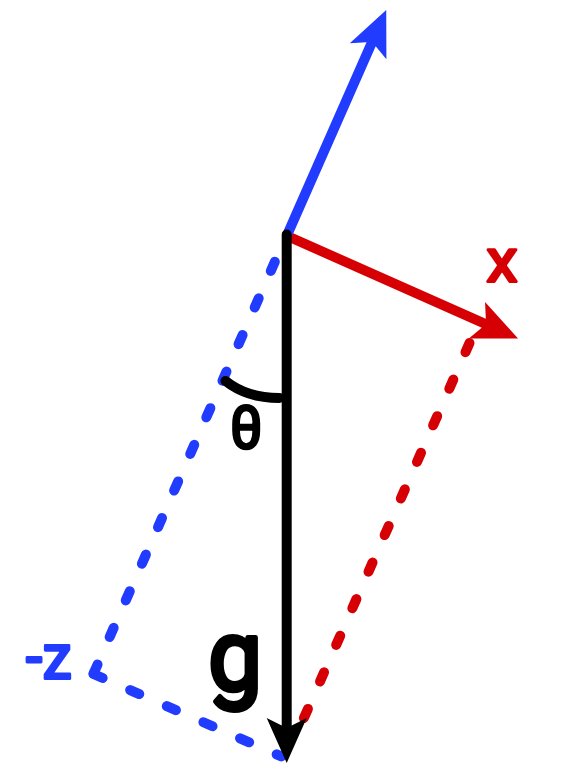De zwarte pijl is de versnelling als gevolg van de zwaartekracht, en de rode en blauwe pijlen zijn de x- en z-assen van het coördinatensysteem van de (gekantelde) sensor.

Accelerometermetingen zijn echter niet nuttig om de oriëntatie te bepalen wanneer de sensor accelereert, omdat dan de gemeten vector niet meer precies naar beneden wijst (in het globale coördinatensysteem).

Gyroscopen meten hoeksnelheid. Door de hoeksnelheid te integreren, krijg je de hoek.
Er is een voorbehoud: het is onmogelijk om exact te integreren, omdat we alleen metingen hebben op discrete tijdstippen. Dit betekent dat we zoiets als de methode van Euler moeten gebruiken, waarvan bekend is dat deze resulteert in een afwijking van de oriëntatieschatting. Om het nog erger te maken, de meting is luidruchtig, en deze ruis is ook geïntegreerd, wat resulteert in een nog grotere fout.

Gelukkig kun je beide onvolmaakte metingen combineren tot een enkele, betere oriëntatieschatting met behulp van een sensor fusie-algoritme. Ik heb met succes het algoritme van Sebastian Madgwick gebruikt voor mijn quadcopter.
Het gebruikt de metingen van de versnellingsmeter om gyro-drift te minimaliseren.

Merk op dat dit algoritme quaternionen gebruikt in plaats van Euler hoeken (rollen, stampen, gieren), omdat deze laatste last hebben van cardanische vergrendeling en omdat quaternionen in het algemeen minder verwerkingskracht nodig hebben.

Merk ook op dat je de gierhoek niet kunt bepalen met de versnellingsmeter, dus je kijk wat af van die meting.

Het is een goed idee om al je berekeningen uit te voeren met quaternionen. Je hebt waarschijnlijk geen Euler-hoeken nodig voor je quadcopter, behalve misschien voor foutopsporing.

Als je wilt, kun je de quaternion ook rechtstreeks uit de versnellingsvector halen:

  Quaternion quaternionFromDirection (Vec3f v) {/ * * Formule: * q = cos (ϑ / 2) + sin (ϑ / 2) · (x · i + y · j + z · k) * waarbij (xyz) een eenheidsvector is die de as vertegenwoordigt waarom * het lichaam is gedraaid; ϑ is de hoek waarmee het wordt gedraaid. * * Bron: * https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation#Using_quaternion_as_rotations * * De rotatie-as (x y z) kan worden berekend door het genormaliseerde * kruisproduct van (0 0 1) en de gegeven vector te nemen. De draaihoek * ϑ vind je met | A × B | = | A || B | · zonde (ϑ). * / // Controleer eerst het randgeval waarbij v == (0 0 z), d.w.z. verticaal if (v.x == 0 && v.y == 0) return {1, 0, 0, 0}; // Bereken het kruisproduct en de norm. Vec3f kruis = {v.y, -v.x, 0}; zweven crossNorm = cross.norm (); kruis / = crossNorm; // Bereken de hoek ϑ. zwevende hoek = std :: asin (crossNorm / v.norm ()); // Bereken het resulterende quaternion. retourneer {std :: cos (hoek / 2), // std :: sin (hoek / 2) * cross.x, // std :: sin (hoek / 2) * cross.y, // std :: sin (hoek / 2) * cross.z, //}; }