De jouwe is een klassiek probleem van kloksynchronisatie . U hebt een softwareklok (het idee van uw programma van de huidige tijd) die u synchroon wilt houden met een referentiehardwareklok (de RTC). Dit wordt doorgaans bereikt door een fasevergrendelingslus of PLL te gebruiken. Het werkt als volgt:
- u meet het verschil tussen de tijd van uw softwareklok en de referentietijd
- u past uw softwareklok aan op basis van deze meting.
Dit is in wezen wat u al aan het doen bent, behalve dat u uw klok vastlegt door deze abrupt te laten stappen, terwijl een PLL de klok gewoonlijk zou laten draaien om deze geleidelijk te synchroniseren.
Stappen op de klok heeft enkele ongewenste effecten: het maakt de tijd onderbroken en, erger nog, het kan het niet-monotoon maken. Ik zou je daarom aanraden om in plaats daarvan je klok te draaien.
Dit is de benadering die ik zou proberen als ik in jouw schoenen zou staan. Ik neem aan dat je een Arduino Uno gebruikt, of een soortgelijk op AVR gebaseerd bord met een 16-bit Timer 1:
- configureer Timer 1 in modus 4: CTC-modus met TOP = OCR1A
- zet de presaler op 64 en OCR1A = 12499 om een periode van 50 ms te krijgen; TIMER1_COMPA_vect zal je onderbreking voor het verzamelen van gegevens zijn.
- configureer je RTC om een 1 Hz output te genereren, en stuur dit signaal naar de input capture pin ICP1 (pin 8 op de Uno)
- voer de PLL uit logica binnen TIMER1_CAPT_vect.
Aangezien de 1 Hz-periode van de RTC een veelvoud is van de timerperiode, zou je verwachten dat de invoerregistratie-eenheid van de timer altijd dezelfde waarde vastlegt. Het verschil tussen twee opeenvolgende vastgelegde waarden is dus een directe maat voor het verloop van uw klok in eenheden van 4 ppm (4 µs / s). De ISR zou in principe als volgt zijn:
ISR (TIMER1_CAPT_vect) {static uint16_t last_capture; uint16_t this_capture = ICR1; int16_t drift = this_capture - last_capture; last_capture = this_capture; // Verlaag de drift modulo 12500 in [-6250, +6250).
if (drift > = 6250) drift - = 12500; if (drift < -6250) drift + = 12500; tune_clock (drift);}
waarbij tune_clock () uw PLL-algoritme is dat verantwoordelijk is voor het draaien van de softwareklok.
Let op de ondertekening van de variabelen. Het aftrekken van de vastgelegde waarden moet worden gedaan met niet-ondertekende getallen, dan het resultaat moet ondertekend worden gemaakt.
Bewerken : zoals voorgesteld door James Waldby, ik zal hier enkele suggesties geven voor de implementatie van de PLL. Het blijkt niet zo eenvoudig te zijn: meten een klokdrift is gemakkelijk, voorspellen is moeilijker.
Laat me het probleem nog eens herhalen. Je hebt een "goede" klok: het RTC 1 Hz-signaal, verondersteld perfect te zijn, maar met een beperkte resolutie van een seconde. En je hebt een "slechte" klok: Timer 1, die een resolutie van 4 µs heeft, maar lijdt aan onnauwkeurigheid van de frequentie, instabiliteit en gevoeligheid voor temperatuur en voedingsspanning. Je wilt beide klokken combineren tot een softwareklok die de goede klok volgt en toch de superieure resolutie van de slechte klok heeft.
Ik zal de volgende notaties gebruiken:
- t is de tijd van de referentieklok (de RTC), waarvan wordt aangenomen dat het ook de fysieke tijd is
- n = ⌊t⌋ is het gehele deel van t, wat ook de tijd is waarop we voor het laatst een update van de RTC hebben gekregen (een timer capture event)
- t ′ is de tijd vanaf de lokale klok (de Arduino-timers)
- x = t ′ - t is de lokale klokoffset, gemeten door de ISR boven een geheel getal waarden van t; de fysieke tijd wordt gegeven door t = t ′ - x
- y = dx / dt is de lokale klokdriftsnelheid; het is een dimensieloze hoeveelheid en typisch minder dan 10 −3 (dwz minder dan 1 ms / s)
- x e (t) is de schatting, gemaakt door de software, van de offset x (t)
- y e (t) = dx e / dt is de schatting van de driftsnelheid y (t)
- t e = t ′ - x e (t e ) is onze softwareklok: een zelf- consistente schatting van t
De eenvoudigste oplossing, die equivalent is aan degene die u in uw vraag hebt, is om aan te nemen dat x constant blijft totdat deze wordt bijgewerkt. Dus
x e (t) = x (n)
t e = t ′ - x (n)
Met andere woorden, we corrigeren alleen voor de laatst bekende offset. Het probleem is, zoals eerder vermeld, dat dit een discontinue tijdschaal oplevert.
Een betere oplossing is om te proberen x (n + 1) te voorspellen en lineair te interpoleren tussen onze vorige en onze huidige voorspelling, waardoor een continue stuksgewijze lineaire schatting van x wordt opgebouwd:
x e (t) = x e (n) + (t − n) y e (n + ½), waarbij y e (n + ½) = x e (n + 1) - x e (n)
Hieruit kan de geschatte tijd worden opgelost voor:
t e = n + (t′− x e (n) −n) / (1 + y e (n + ½)) ≈ n + (t′ − x e (n) −n) ⋅ (1 − y e (n + ½))
De factor 1 / (1 + y e (n + ½)) ≈ (1 − y e (n + ½)) verklaart het feit dat de klok is gedreven sinds de laatste update op t = n.
Nu zijn we links met het probleem van het voorspellen van x (n + 1). Er zijn veel mogelijke benaderingen, en ik zal proberen er maar een paar te beschrijven.
Simpele PLL
Een eenvoudige benadering is het simuleren van een analoge PLL met een eerste-orde-laagdoorlaatfilter. Hier is de eerste illustratie van het Wikipedia-artikel over fasevergrendelde lus:

Er is enige vertaling nodig tussen deze analoge afbeelding en het digitale domein: De fasevergelijker neemt het verschil tussen de gemeten verschuiving x (n) en onze vorige voorspelling x e (n). Het laagdoorlaatfilter wordt geïmplementeerd als een exponentieel gewogen voortschrijdend gemiddelde. De output van het filter is onze schatting van de driftsnelheid: y e . De VCO is de formule voor het schatten van t e , die de ingebouwde driftsnelheid heeft −y e . Dit zou ruwweg als volgt naar C ++ kunnen worden vertaald:
struct {uint32_t n; // tijd van laatste update
zweven xe; // schatting van de offset op het moment n float ye; // schatting van de driftsnelheid voor t in [n, n + 1]} klok const float tau = 60; // laagdoorlaatfilter tijdconstante, in secondenconst float K = 1; // DC-versterking van de filterconst float alpha = 1 / (1 + tau); // Geroepen door de ISR. // y is (x [nu] - x [1 seconde geleden]) in eenheden van 4 us. Vermijd tune_clock (int16_t y) {statische float x; // laatst bekende verschuiving x + = y * 4e-6; // update bekende offset float xe = clock.xe + clock.ye; // schatting van de huidige offset // Update tijd. klok.n ++; // Update onze schatting van de driftsnelheid. clock.ye + = alpha * (K * (x-xe) - clock.ye); // Update of schatting van de offset. clock.xe = xe;} // Schat de huidige time.float time () {float t_local = micros () * 1e-6; return clock.n + (t_local - clock.xe - clock.n) * (1 - clock.ye);}
Merk op dat de bovenstaande code alleen bedoeld is als richtlijn. Een goede implementatie zou fixed-point moeten gebruiken in plaats van floats en zou ook berollover-safe moeten zijn.
De tijdconstante van het filter moet groot genoeg worden gekozen om de jitter, veroorzaakt door de resolutie van 4 µs, te verminderen, maar tegelijkertijd ook kort genoeg volg de frequentievariaties van de lokale klok. Idealiter zou het dicht bij het Allan intercept van de x (n) tijdreeks moeten zijn.
Dit soort PLL doet normaal gesproken goed werk bij het volgen van de referentieklok, maar het heeft er een nadeel: het heeft de neiging om een systematische offset te dragen. Laten we voor de eenvoud aannemen dat de driftsnelheid constant is. Dan is het gemakkelijk te zien dat de stabiele toestand van de PLL een afwijking heeft:
t e - t = x - x e = y / K
waarbij K de DC-versterking van het filter is. Een grote versterking minimaliseert deze fout, maar dit gaat ten koste van de stabiliteit. Een te grote DC-versterking en de PLL zal spontaan in grote oscillaties gaan.
Ik neem aan dat het mogelijk moet zijn om van deze systematische vertekening af te komen door meer geavanceerde filters te gebruiken, misschien zoiets als een PID, maar ik
willen niet in de complexiteit van dergelijke filters duiken.
Eenvoudige lineaire extrapolatie
Een andere manier om x (n + 1) te schatten, die geen last heeft van systematische afwijkingen, is door lineair extrapoleer uit de twee laatst bekende waarden:
x e (n + 1) = 2 x (n) - x (n − 1)
Dit betekent dat we aannemen dat de driftsnelheid constant is op deze korte tijdschaal. Het probleem met deze methode is dat het de neiging heeft om de fluctuaties als gevolg van de jitter te versterken. Uitgaande van bijvoorbeeld een (te optimistische) driftsnelheid van 2 ppm, zal de gemeten offset afwisselen tussen nul en 4 µs incrementen. De extrapolatie voorspelt dat elke nulstap wordt gevolgd door een nieuwe nulstap, en elke 4 µs stap wordt gevolgd door een nieuwe 4 µs stap, en dus zal het altijd fout zijn. De tijdevolutie zou er als volgt uitzien:
t [s] 0 1 2 3 4 5 6 7 8 9 10x [µs] 0 0 4 4 8 8 12 12 16 16 20xₑ [µs] 0 0 0 8 4 12 8 16 12 20 16
Brown's lineaire exponentiële afvlakking
Brown's methode is een van de vele lineaire extrapolatiemethoden die bedoeld zijn om ruis in de gegevens weg te werken. Het is gebaseerd op het tweemaal uitvoeren van hetzelfde laagdoorlaatfilter op de invoergegevens:
s1 = low_pass (x) // eerste afvlakking2 = low_pass (s1) // tweede afvlakking
Als τ de tijdconstante van het filter is, dan is s 1 een gemiddelde van gegevens die , gemiddeld de leeftijd τ, terwijl s 2 de leeftijd 2τ heeft. Wanneer kan dan, op tijdstip t, een lineaire extrapolatie uitvoeren door een rechte lijn door de punten (t − τ, s 1 ) en (t − 2τ, s 2 ) te laten lopen . Dit geeft het volgende algoritme voor het bijwerken van de schattingen van de offset en de driftsnelheid:
statische float s1, s2; // x eenmaal en tweemaal afgevlakt1 + = alpha * (x - s1); // update s1s2 + = alpha * (s1 - s2); // update s2
// Update of schatting van de offset.clock.xe = xe; // Extrapoleer om de volgende offset te schatten.xe = s1 + (s1-s2) * (tau + 1) / tau; // Update onze schatting van de driftsnelheid .clock.ye = xe - clock.xe;
Ook hier zou de optimale tijdconstante in de orde van de Allan-onderschepping moeten zijn. Merk op dat de limiet τ → 0 de eenvoudige extrapolatie geeft van de vorige sectie.
De onderstaande afbeelding toont de prestaties van dit algoritme op gesimuleerde gegevens. De gesimuleerde klok heeft een driftsnelheid die oscilleert tussen 1,7 en 2,3 ppm, en de gemeten offset wordt afgerond op het dichtstbijzijnde veelvoud van 4 µs. De regel met het label "voorspeld (τ = 0)" is de eenvoudige extrapolatie van de vorige sectie:
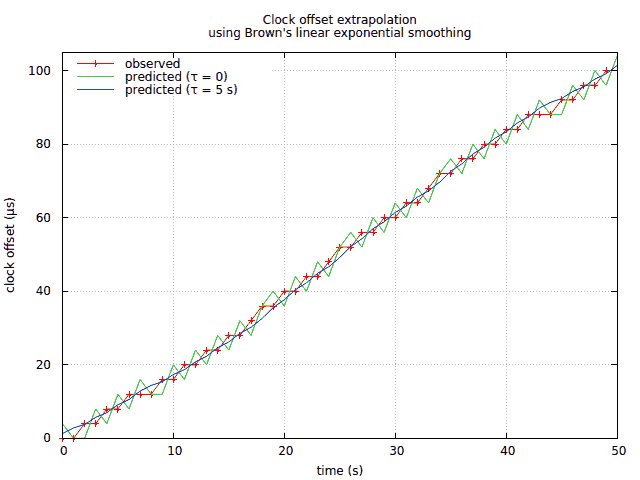
Hier is de grote jitter van de eenvoudige extrapolatiemethode vrij duidelijk. Op deze gesimuleerde gegevens werkt de methode van Brown goed met een tijdconstante in de orde van 5 s. De frequentie van een echte klok zou veel langzamer veranderen, en een langere tijdconstante zou beter werken.
Dit is waarschijnlijk allemaal te algemeen voor uw specifieke gebruikssituatie. Ik wist niet wanneer ik met deze bewerking begon, het zou me zo ver leiden ... Als je meer dan bijvoorbeeld 10 µs jitter kunt verdragen, dan zou de simpele extrapolatie goed genoeg moeten zijn. En als u alleen de tijd att′-periodieke intervallen nodig heeft, kan dit enkele optimalisaties mogelijk maken.